Deep Learning Preliminary Knowledge(3):Linear Algebra

标量

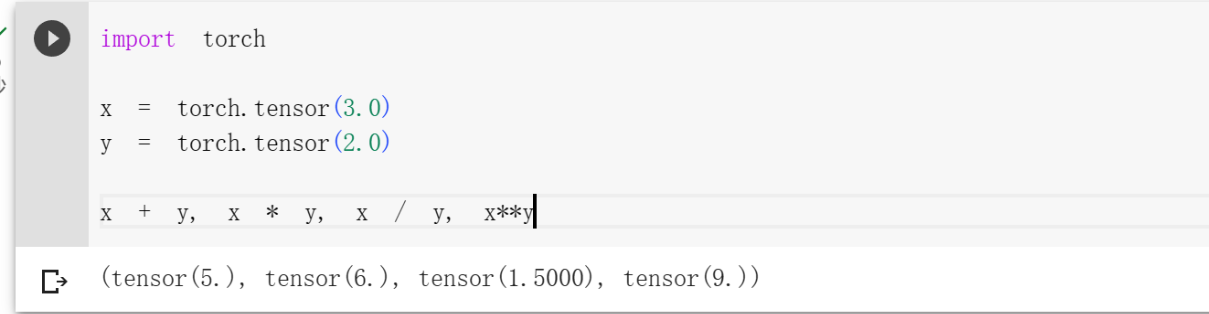
标量是只有大小、没有方向的量。可以进行算术运算，即加减乘除、指数等运算。

import torch

x = torch.tensor(3.0)
y = torch.tensor(2.0)

x + y, x * y, x / y, x**y

向量

向量是指具有大小和方向的量。向量可以被视为标量值组成的列表.
可以通过下标来访问向量的任意元素，x[ n ]。
向量的长度通常称为向量的维度，可以通过python通过的len函数或者 .shape属性访问向量的长度。

import torch

x = torch.arange(4)

print(len(x))
x.shape

向量可以点积操作，用 x T y表示，是相同位置的按元素乘积的和。

import torch

x = torch.arange(4,dtype=torch.float32)
y = torch.ones(4,dtype=torch.float32)
x,y,torch.dot(x,y),torch.sum(x * y) 

矩阵

矩阵，数学术语。在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。 可以通过行索引和列索引（Matrix[i][j]）来访问矩阵元素，注意：这里是从0开始的。

转置

当我们交换矩阵的行和列时，结果称为矩阵的转置（transpose）。 通常用来表示矩阵的转置，如果 ,则对于任意 和 ,都有

import torch

A = torch.arange(20).reshape(5, 4)
A,A.T

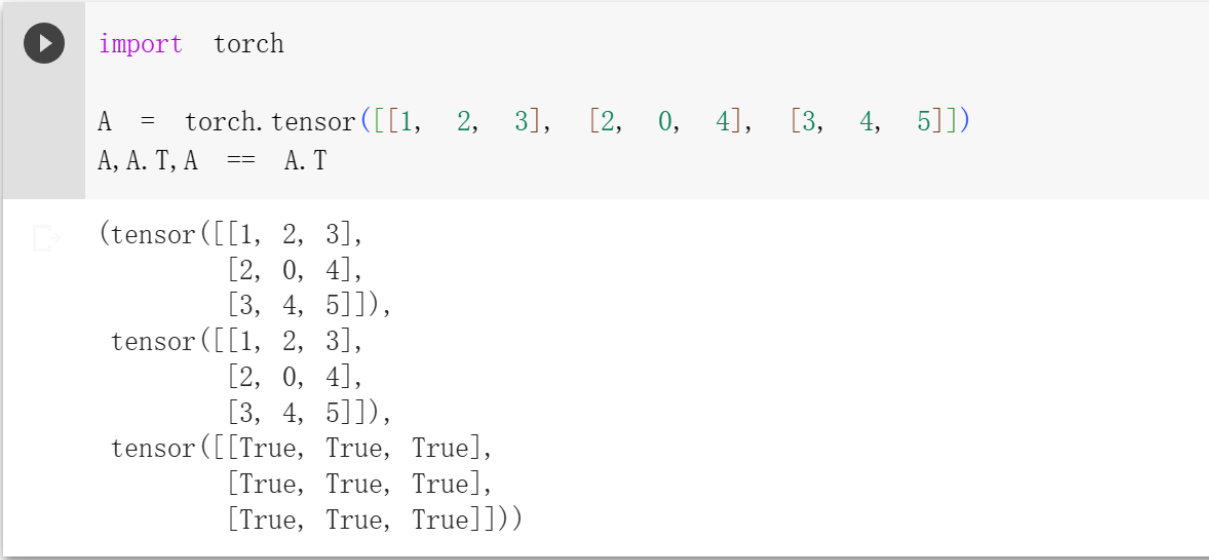
作为方阵的一种特殊类型，对称矩阵（symmetric matrix）, 等于其转置 。

import torch

A = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
A,A.T,A == A.T

矩阵-向量积

矩阵-向量积：一个矩阵(m * n)乘以一个列向量(n * 1)，得到的结果是行向量(m * 1)；一个矩阵(m * n)乘以一个行向量(1 * n)，得到的结果是列向量(1 * m)。
注意

• 乘以行向量时，只有矩阵的列数与行向量的列数一样时，才能进行矩阵-向量积。
• 乘以列向量是，只有矩阵的列数与列向量的行数相等时，才能进行矩阵-向量积。

运算规则
将矩阵的每一行元素乘以向量的行元素

将矩阵的每一行元素乘以向量的列元素

import torch

X = torch.arange(12).reshape(3,4)
a = torch.tensor([1,3,4,5]) #矩阵的列数 与 行向量的列数一样
X,a,X.shape,a.shape,torch.mv(X,a)

矩阵-矩阵乘法

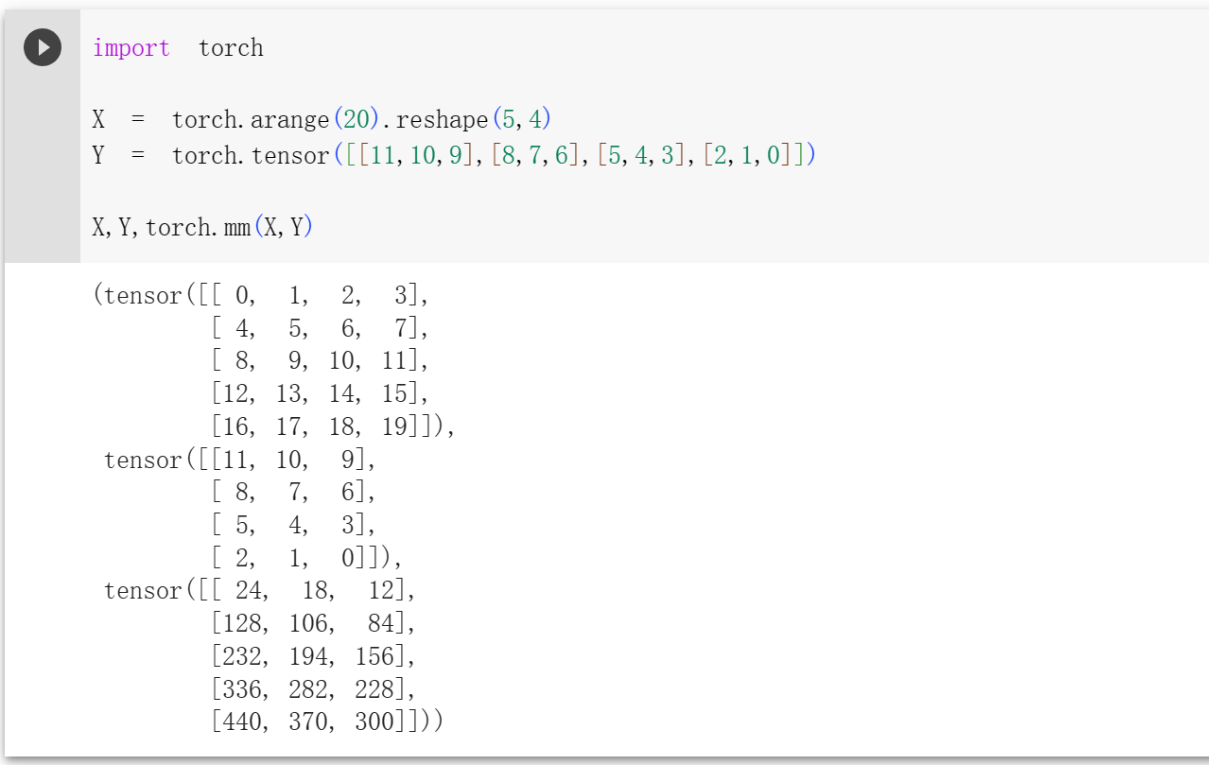
就是矩阵A（m * n）与矩阵B（n * k）相乘，得到一个m * k的矩阵C。只有在第一个矩阵的列数（column）和第二个矩阵的行数（row）相同时才有意义。 此时有两个矩阵

咱们用行向量 表示矩阵 的每一行，用列向量 表示矩阵 的每一列，那么则有

那么结果 就等于 的行向量 乘以 的列向量。表示转置成列向量，这样才能计算点积

张量

就像向量是标量的推广，矩阵是向量的推广一样，张量 是描述具有任意数量轴的维数组的通用方法，目的是把向量、矩阵推向更高的维度。例如，向量是一阶张量，矩阵是二阶张量。

给定具有相同形状的任意两个张量，任何按元素二元运算的结果都将是相同形状的张量。 例如两个矩阵相加

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
A, A + B

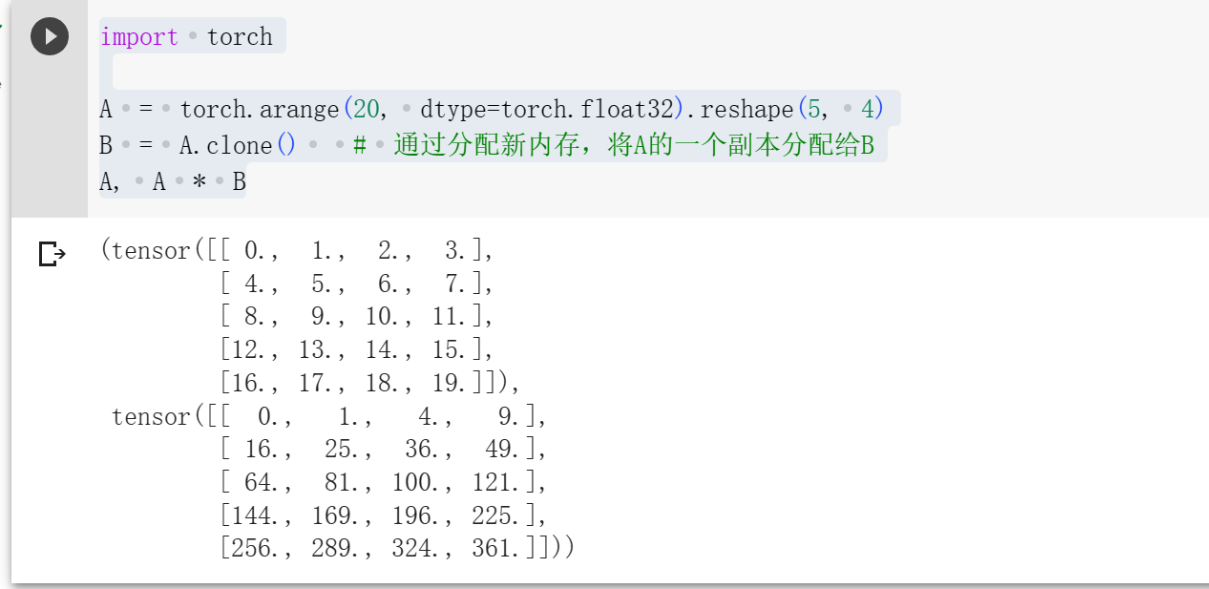
两个矩阵的按元素乘法称为Hadamard积。比如 ，那么任意的 都满足

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
A, A * B

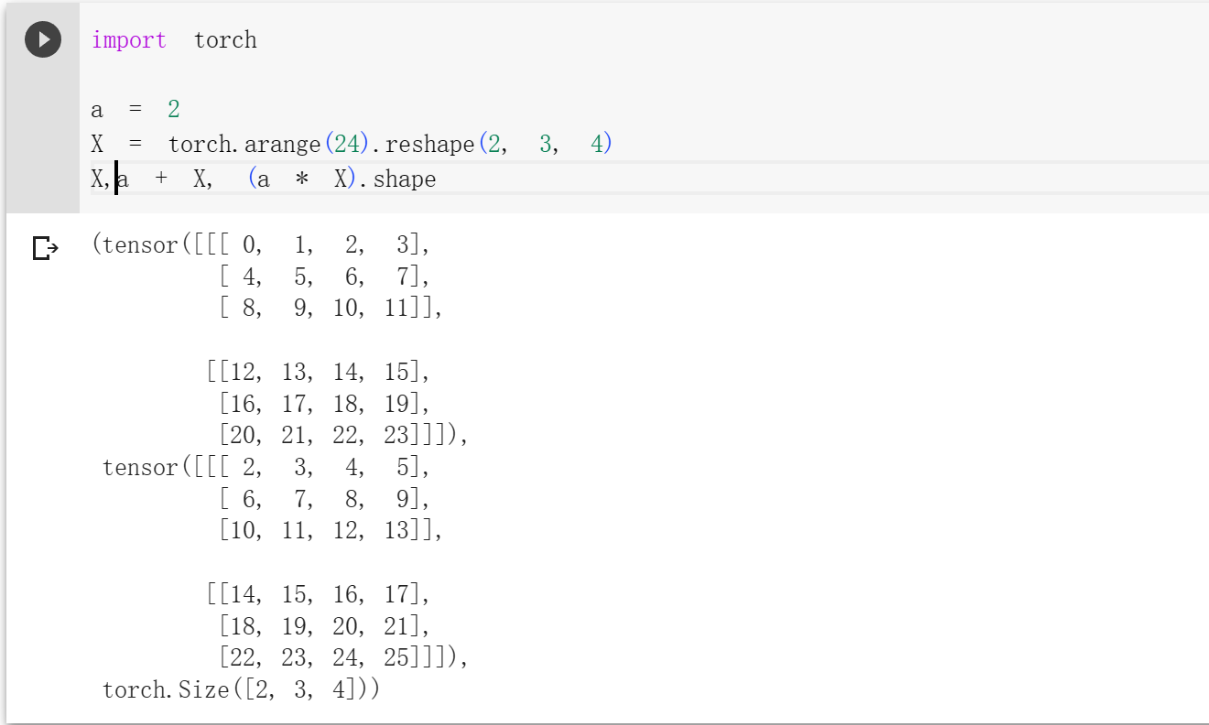
将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。

import torch

a = 2
X = torch.arange(24).reshape(2, 3, 4)
X,a + X, (a * X).shape

降维

我们可以对任意张量进行的一个有用的操作是计算其元素的和。使用sum函数即可，对应向量量(长度为d)的求和用数学表示就是 ,对应矩阵(m * n)的求和就是

import torch

x = torch.arange(4, dtype=torch.float32)
y = torch.arange(12).reshape(3,4)
x, x.sum(),y,y.sum()

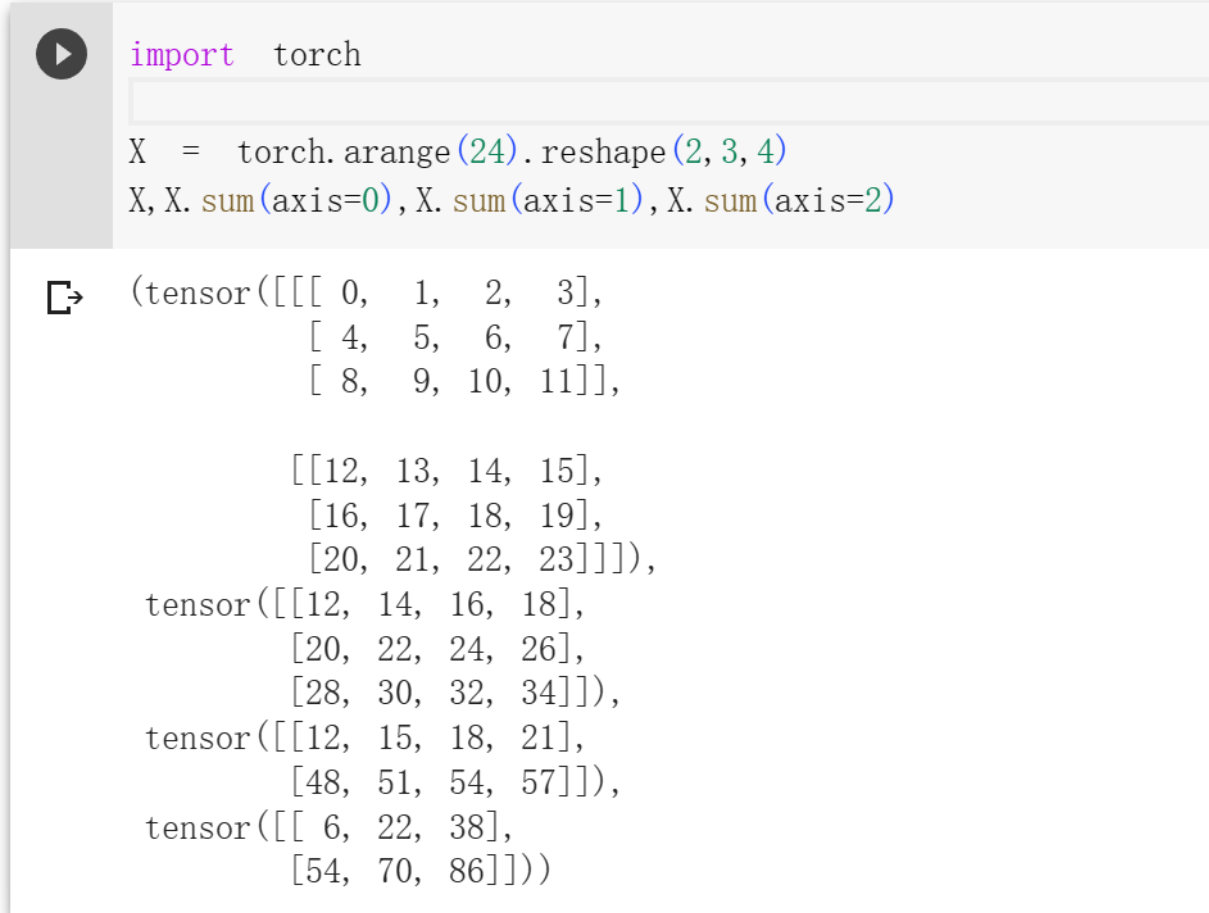
默认情况下，调用求和函数会沿所有的轴降低张量的维度，使它变为一个标量。 我们还可以指定张量沿哪一个轴来通过求和降低维度。 以矩阵为例，为了通过求和所有行的元素来降维（轴0为行，轴1为列）。

import torch

x = torch.arange(12).reshape(3,4)
x,x.sum(axis=0),x.sum(axis=1)

应该不难看出来是如何求和的吧。在矩阵中，对轴0求和，就是把行的维度去掉，只有列，每一列求和得到结果；轴1求和，把列的维度去掉，只有行，对每一行进行求和.
那么三阶张量是如何指顶轴进行求和的呢？首先先来指定三个维度是什么，第一个维度是矩阵个数，第二个维度是每一个矩阵中的行数，第三个维度是每一个矩阵中的列数。
当对第一个维度求和时，此时应该把所有矩阵压缩为一个矩阵。假设第一个维度为2，由两个矩阵A、B组成，那么结果应该满足

对第二个维度进行求和时，即对每一列进行求和得到一个数，就成了行。
对第三个维度进行求和时，即对每一行进行求和得到一个数，就成了列。

import torch

X = torch.arange(24).reshape(2,3,4)
X,X.sum(axis=0),X.sum(axis=1),X.sum(axis=2)

同时也可以对多个维度进行降维求和，求和顺序按照写的顺序即可，注意：如果数字相同、顺序不同，那么结果仍然是相同的。
举例，现在有一个(2,3,4)的张量，对[0,2]的维度进行求和，那么过程是什么呢？
先对第一个维度进行求和，得到一个(3,4)的张量，在对第二个维度（我理解的是本来是第三个维，但是消除了一维，那么应该对应减1）进行求和，得到 (3)的张量

import torch

X = torch.arange(24).reshape(2,3,4)
X,X.sum(axis=0),X.sum(axis=[0,2])

---

但是有时候降维求和不是一件好事，对进行算法操作不是很好，由于少了维度，所以无法通过广播来进行运算。所以咱们需要保持轴数不变进行求和，很简单，只需要在sum()里面加上一个keepdims=True即可。

import torch

X = torch.arange(12).reshape(3,4)
Y = X.sum(axis=0)
Z = X.sum(axis=0,keepdims=True)
Y,Z,Y.shape,Z.shape

范数

范数（norm）是对向量（或矩阵）大小的一个度量方式。它描述了向量的长度、大小或距离，并通常表示为函数形式

其中，在 范数中常常省略下标2，也就是说等同于。 在代码中，我们可以按如下方式计算向量的范数。

u = torch.tensor([3.0, -4.0])
torch.norm(u)

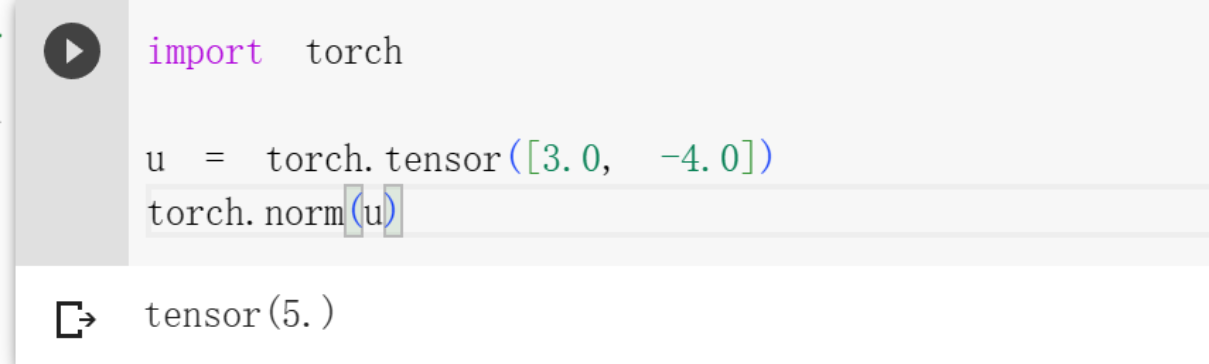
深度学习中更经常地使用 范数的平方，也会经常遇到 范数，它表示为向量元素的绝对值之和

import torch

u = torch.tensor([3.0, -4.0])
torch.norm(u),torch.abs(u).sum()