Deep Learning Preliminary knowledge(4):Calculus

导数和微分

导数的计算是所有深度学习优化算法的关键步骤。 在深度学习中，我们通常选择对于模型参数可微的损失函数。简而言之，对于每个参数， 如果我们把这个参数增加或减少一个无穷小的量，可以知道损失会以多快的速度增加或减少.
导数的定义 下面是导数的几个等价形式。 其中符号和 是微分运算符，表示微分操作。微分、导数的运算法则就不细说了.

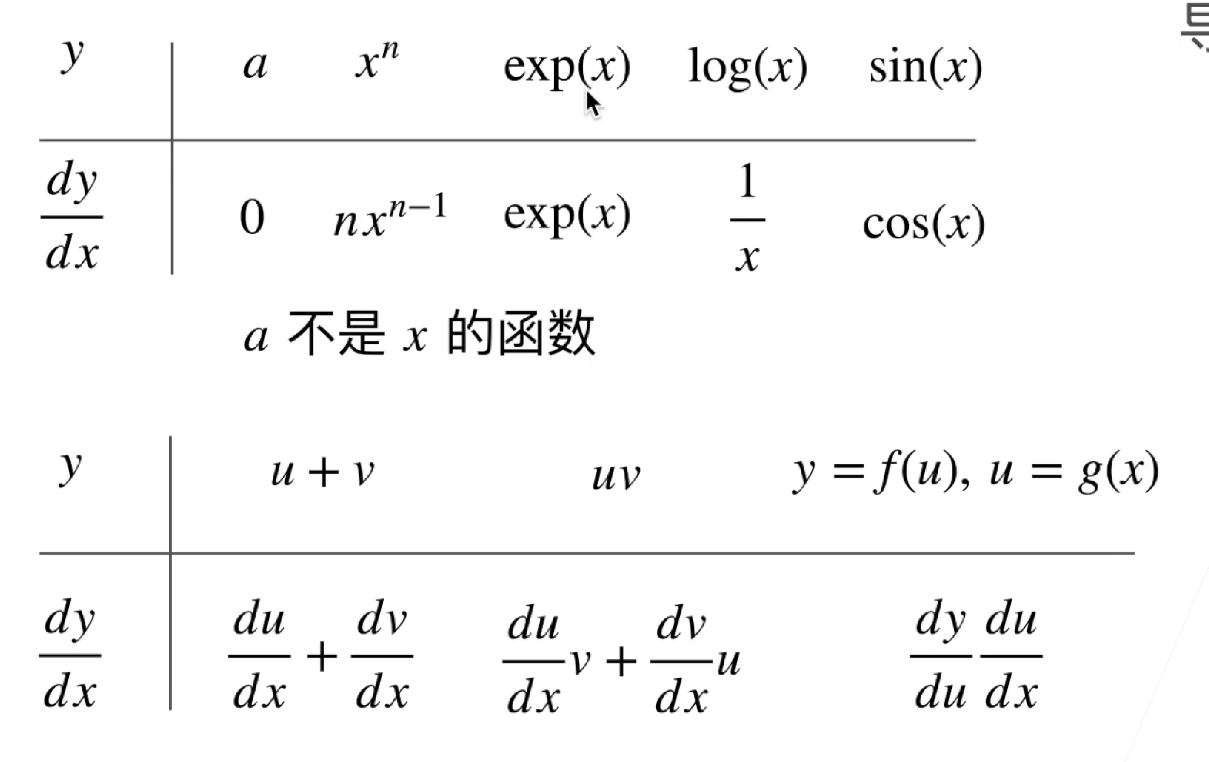
偏导数

定义：一个多变量的函数（或称多元函数），对其中一个变量（导数）微分，而保持其他变量恒定。
这个在深度学习中时非常常见的，函数通常依赖许多变量，可以通过偏导数的方法来看看每一个变量对函数的影响。
一般地，函数f(x1,...,xn)在点(a1,...,an)关于xi的偏导数定义为： 那么偏函数的求导也是十分简单的。
当对某一个参数求偏导时，其他参数都看成常数来处理。

梯度

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

将导数拓展到向量

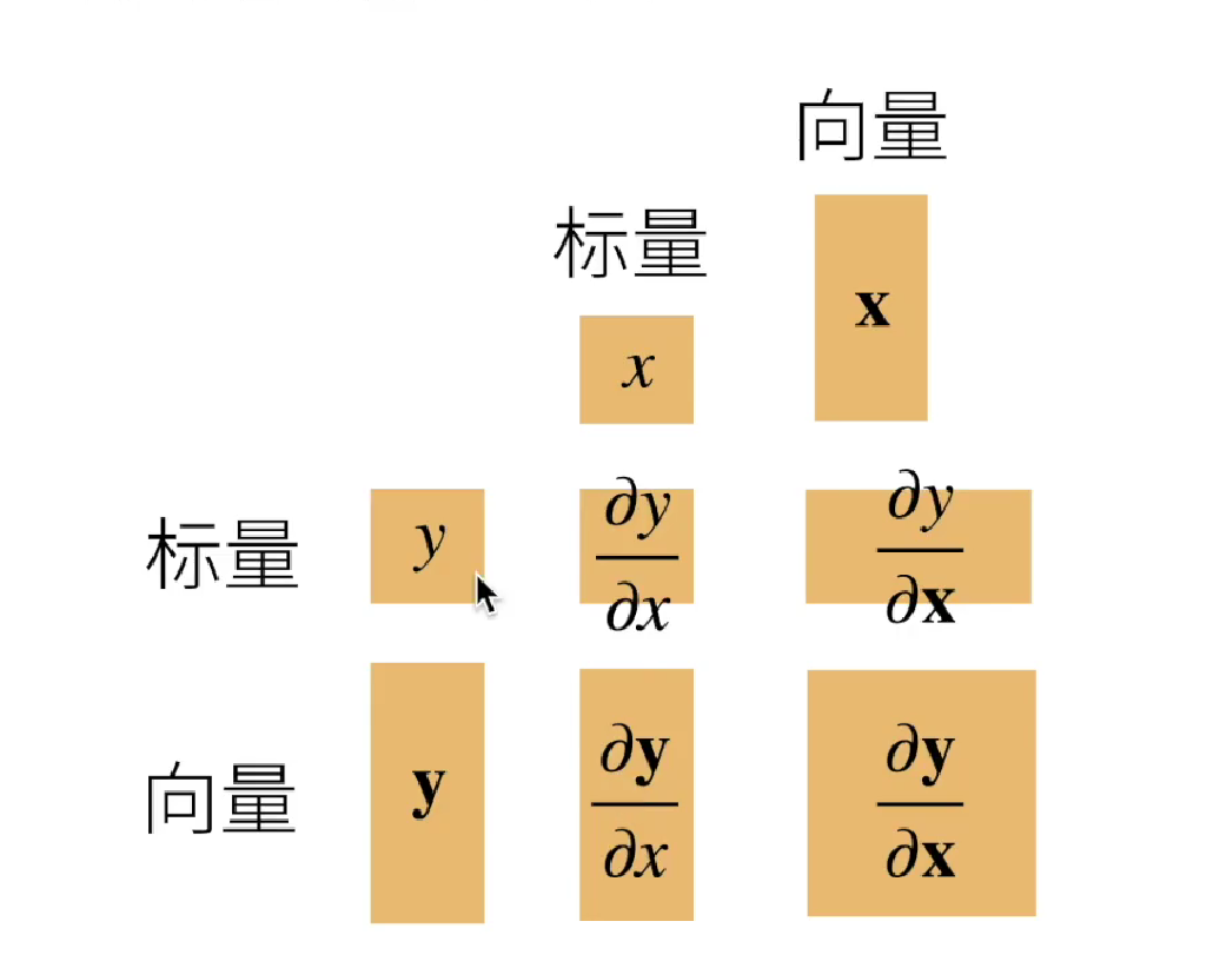
下面来详细说一下这几种情况。

1、当 y 为标量，x为列向量时 那么y对x求偏导，得到的是一个行向量 举个简单的例子
2、当 x 为标量，y为列向量时 那么y对x求偏导，得到的是一个行向量 3、当 y 为列向量，x为列向量时 如果y对x求偏导，那么结果就是一个矩阵。
其实也很简单，看成是一个有一列的标量对列向量求偏导。那么每一个标量y对x求偏导，得到的就是一个行向量。一共有m个变量，所以得到的是 m * n的矩阵。这个也叫做分子布局。

关于矩阵求导、分子布局、分母布局，详细可以看这篇文章 hero

链式法则

但是，现实生活中，函数不可能是单一变量，通常是复合的，难以用上面的公式进行求解。这时候就需要用到链式法则了。

标量

当函数 ,此时对函数 y 用 x 求偏导的结果为 就像剥洋葱那样，一层一层剥。
举例，例如
首先，咱们可以看出来是 由幂函数 + 三角函数组成
那么结果为

向量

首先看一下标量对向量的链式求导
假设最终优化的目标z是个标量，、 是m、n维向量，依赖关系为 -> -> z。现在需要求
那么就结果为 首先，对 求偏导 得到的结果是 (1,n)的行向量，接着 对 求偏导得到的是 (n,m)，最后向量 乘以 矩阵的结果为还是一个（n，m）的矩阵。 接下来再看一下向量对向量求偏导
假设 （1,m）、(1,n)、(1,k)都为向量，有 -> -> 的依赖关系，那么对 求 的偏导的结果为 首先 对 求偏导的结果为 （k，n）的矩阵，对 求偏导的结果为 （n，m）的矩阵，最后得到（k，m）的矩阵。 最后，咱们来看一下例子
、是向量；是标量；表示向量内积 计算
首先，咱们分析一下，
那么z对求w偏导就是 为什么对 、向量的内积求 的偏导等于 (向量 的转置)呢？
这个其实是上面的向量求偏导公式

最后

在这两天学习深度学习里面的数学部分中，我发现和我在学校高数课上学的不一样，是一种什么感觉呢？就是感觉自己好像学过，但是又搞不懂是怎么回事。
高数书让我们进行微分、求偏导的都是一个函数表达式，而深度学习里面却是一个向量/矩阵。
那么如何理解向量呢？
其实向量就是把那些函数表达式里面的未知数的系数提取出来，形成一个数组，这就是向量。
矩阵也是如此，把未知数的系数提取出来，形成一个二维数组。
由于还没有学习线性代数，理解比较浅显。只是为了解决 在学习 深度学习过程中，由向量/矩阵引起的困惑。感兴趣的可以看一下下面这两个文章。 向量的本质问答 矩阵的本质