前言

但是在深度学习的神经网络中，动不动就好多层函数，手写是不太可能的，所以这时候就需要用到自动微分了。
首先，先来了解一下数值微分和符号微分。

数值微分
直接根据微分极限的定义形式只需要在附近区一个很小的 (比如 0.00001)，分别计算和的值，然后做一个减法和除法就能得到此时的微分了，非常的直观.

符号微分
符号微分（Symbolic Differentiation）属符号计算的范畴，其计算结果是导函数的表达式。符号计算用于求解数学中的公式解（也称解析解），得到解的表达式而非具体的数值。和手动微分的不同是，手动微分需要自己求解出表达式，然后编写程序；而这个是通过程序来计算表达式，不需要手算。

自动微分同时结合了“数值微分”和“符号微分”的长处，既对于已知函数直接采用数值微分法求取微分，并作为中间结果保存；对于组合函数采用符号微分法将公示展开，并将上一步数值微分的中间结果代入，二者结合降低了求解和计算的复杂度。

计算图

接下来，我们来了解一下自动微分的工作原理。
第一步：先将代码分解成可操作因子
第二步：将计算表示成一个有向无环图，每一个节点都是一个输入或者操作。

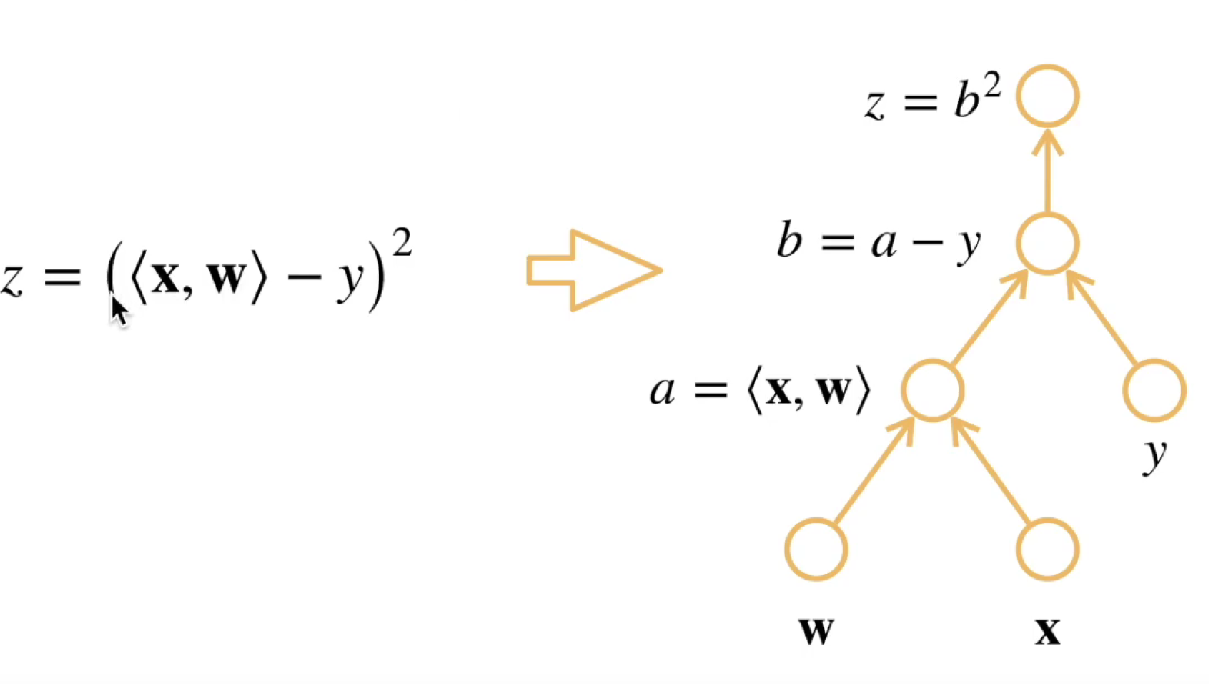
而计算图的构造方式有两种，分别为显式构造、隐式构造。

显示构造
用户需要手动构建计算图。用户可以明确地定义每个操作节点，并将其连接到输入变量和输出变量。类似于数学中，先定义一个公式，然后把具体值带入公式得到结果。

隐式构造
自动微分工具或库会根据用户提供的函数表达式自动生成计算图。用户只需要提供函数的输入和输出，无需手动定义每个操作节点。自动微分工具会根据函数表达式的规则自动构造计算图。

模式

自动微分有两种模式，分别为正向累积、反向累积。
先把链式法则写出来，来生动解释两种模式。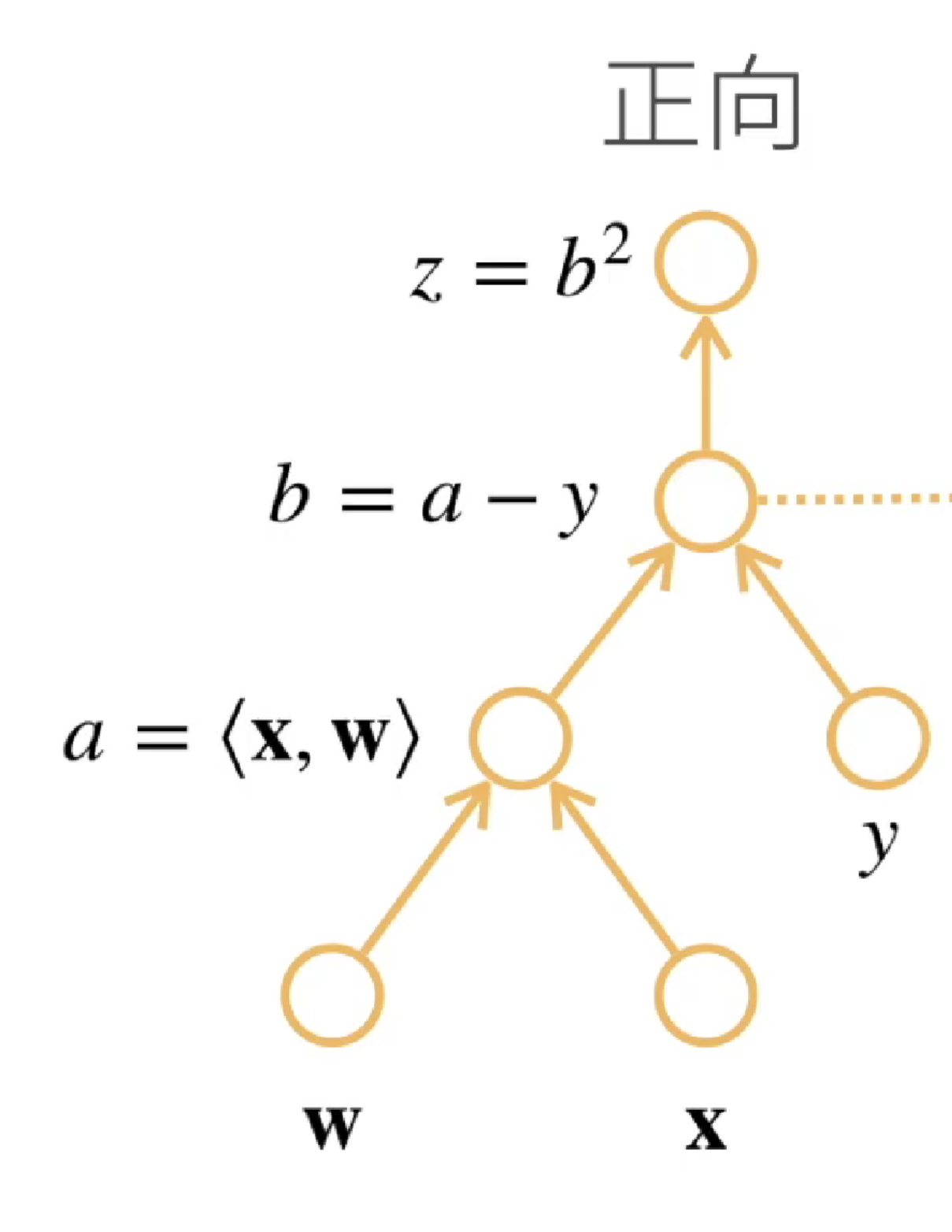
正向累积：是一种从输入到输出的计算模式。按照函数计算的顺序逐步计算函数的值，并将导数传递给下一个操作

反向累积：是一种从输出到输入的计算模式。从输出开始，计算函数的梯度或导数，并以相反的顺序传播它们到每个操作。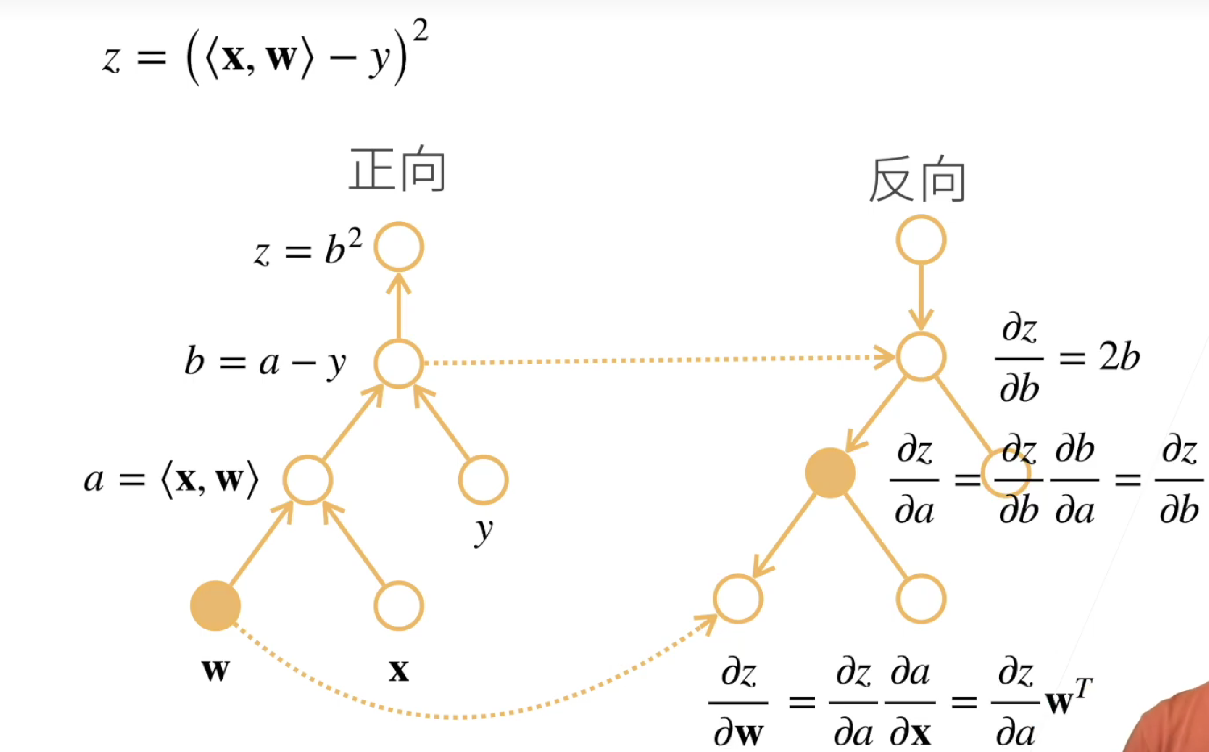

参考文章
python实现自动微分
 自动微分技术
 自动微分

演示

假设我们要对关于求偏导首先，定义一个向量，并为向量分配一个空间来存储梯度。

import torch

x=torch.arange(4.0)
x.requires_grad_(True) # 可以直接写x=torch.arange(4.0,requires_grad=True)
x,x.grad

接下来构建y，

y=2 * torch.dot(x,x)
y

通过调用反向传播函数来自动计算y关于x每个分量的梯度，并打印这些梯度。

y.backward()
x.grad

backward函数讲解
最后用咱们手算的来看看是否计算正确

注意：pytorch对梯队默认累积，每一次计算后要清空。

分离计算

有时，我们希望将某些计算移动到记录的计算图之外。
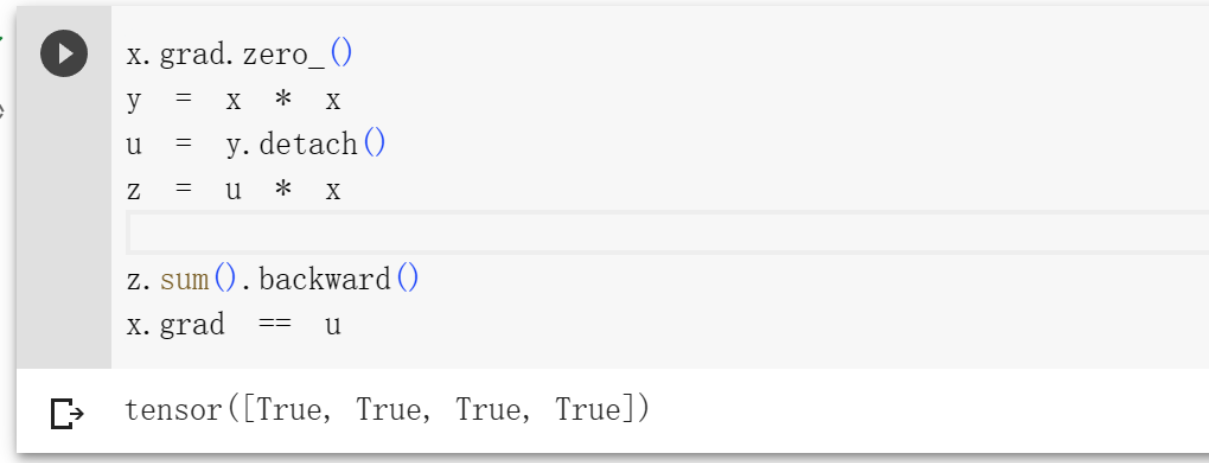
假设y是作为x的函数计算的，而z则是作为y和x的函数计算的，但是不想要计算y的任何信息，那么可以分离 y 来返回一个新变量，保存一样的值，但是没有任何求解的信息。
大概意思就是，y是由x得到的，这里面有计算图，咱们只需要用结果值，不想知道是怎么得到的，那么就用分离y，变成一个常量。

x.grad.zero_()
y = x * x
u = y.detach() #分离
z = u * x

z.sum().backward()
x.grad == u

StarHui Blog

Preliminary knowledge(5):Automatic Differentiation

前言

计算图

模式

演示

分离计算