Linear Regression Experiment

Linear Regression Experiment

StarHui Lv3
  2023-06-21 21:01:17 2023-06-21 21:01:17 Created   2023-11-06 20:05:37 2023-11-06 20:05:37 Updated    1.5k Words  6 Mins  

前言

学完之后，感觉有点不过瘾，所以在网上找了一个csv文件来试试线性回归
波士顿房价数据集
先下载到本地后，接下来就开始吧。

上传数据

由于我用的是colab，所以接下来就讲解colab如何导入cvs文件以及读取。

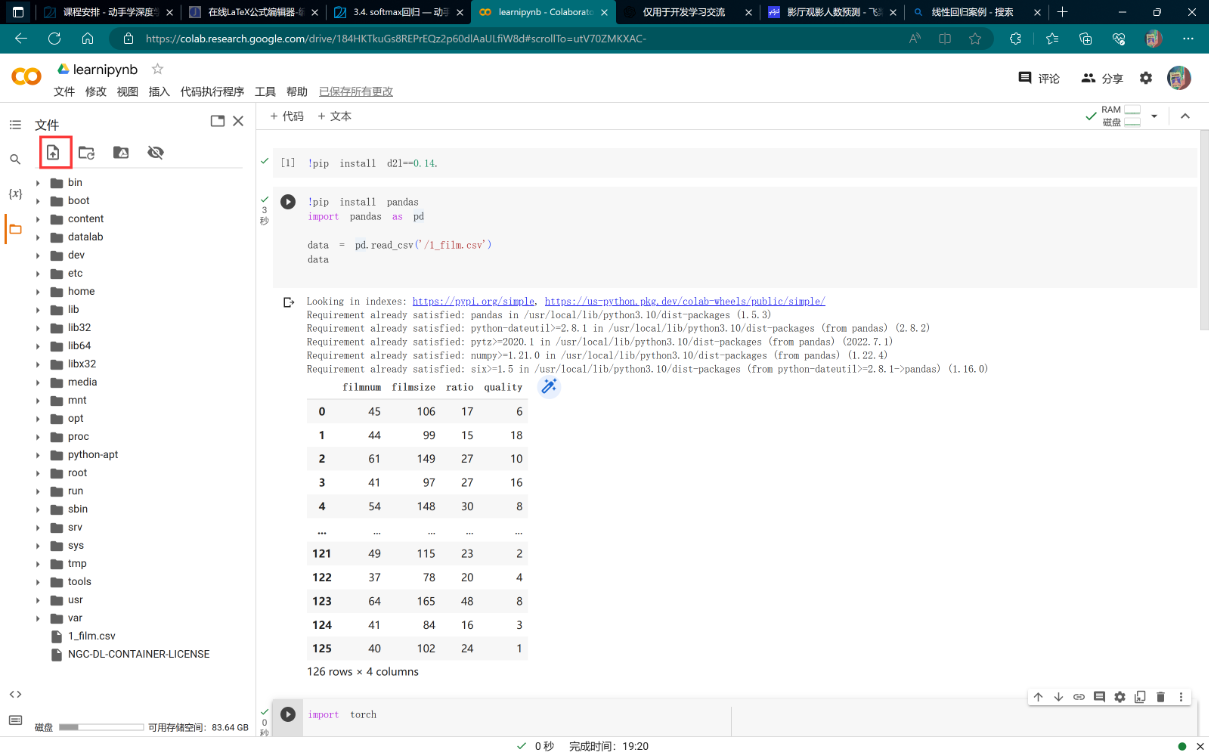
点击上传文件，上传后找到该文件，右键复制路径

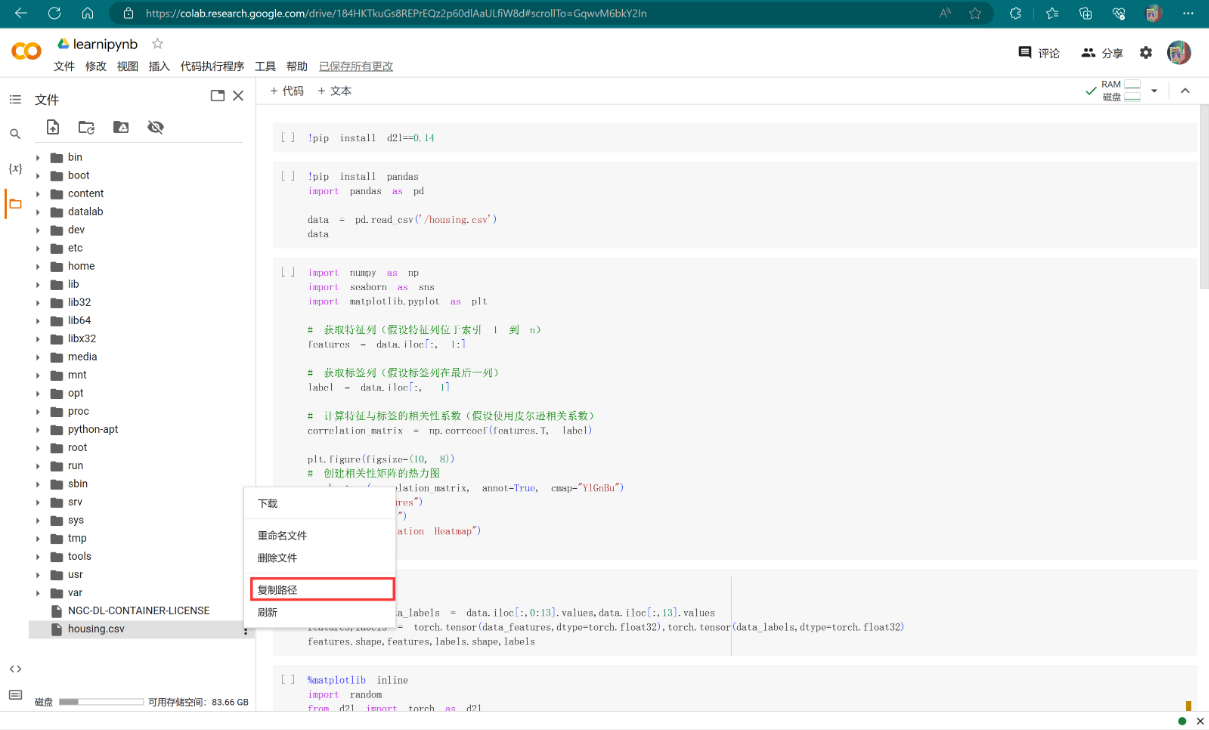
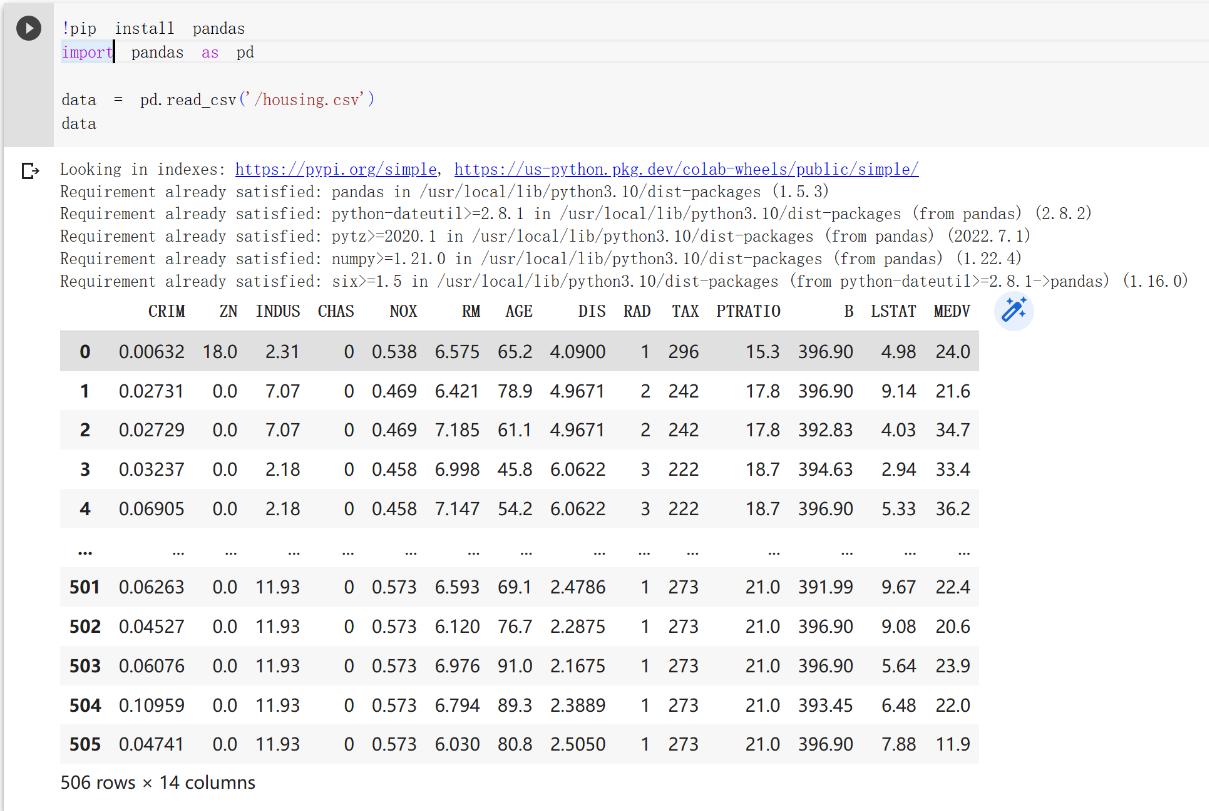
读取数据

1
2
3
4
5
!pip install pandas
import pandas as pd

data = pd.read_csv('/housing.csv') # ''里面的为复制的路径
data

数据预处理

数据清洗

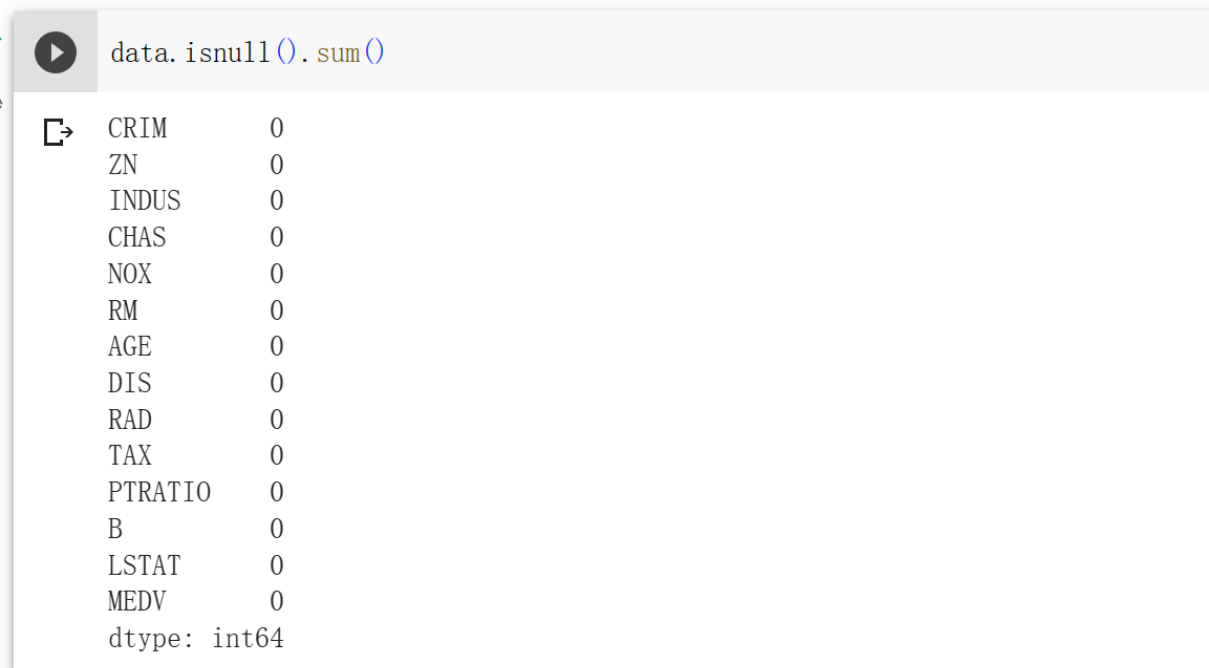
首先看一下有没有空值，可以使用isnull函数查看

1
data.isnull().sum() #sum函数累加统计

以下是各字段的解释，图片来自网络截屏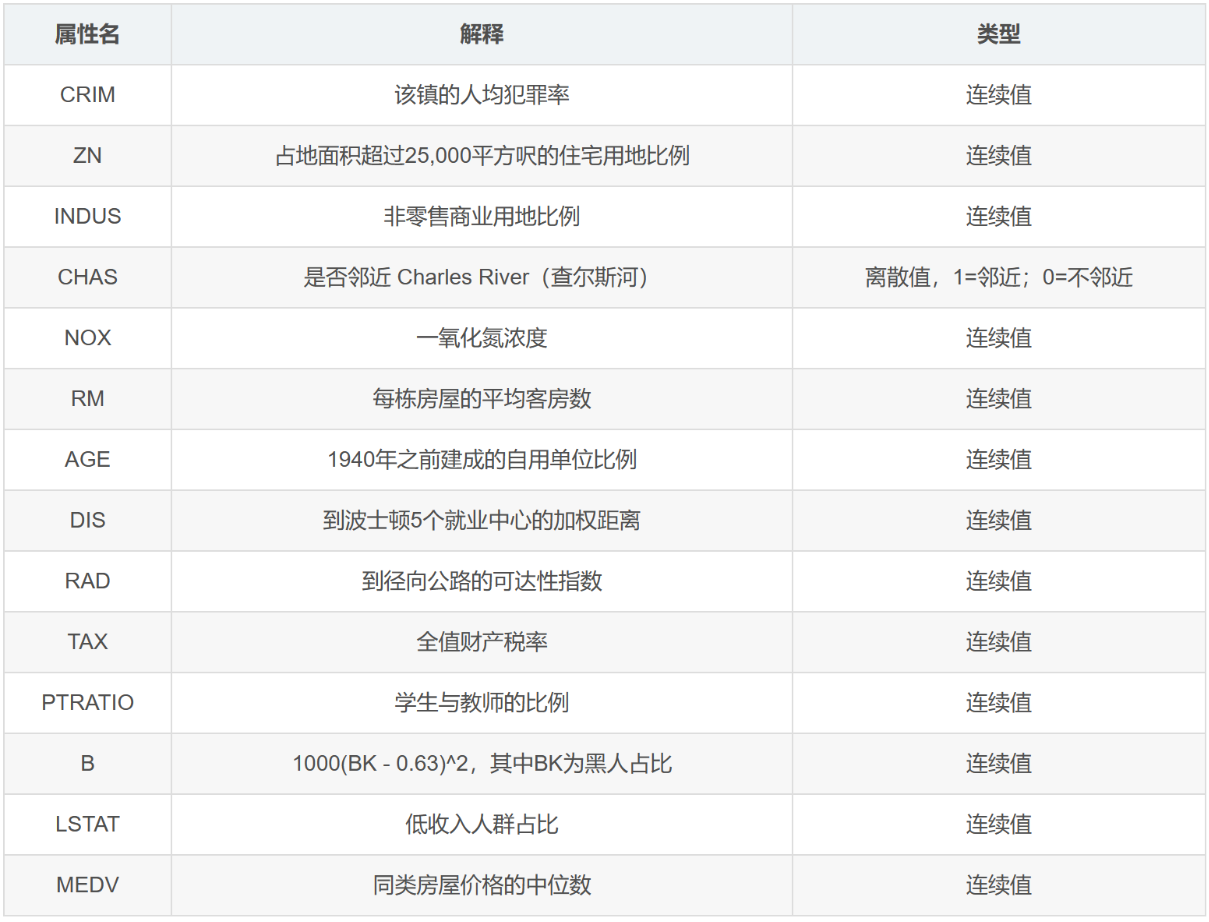

接下来看看是否异常值，使用 describe函数

1
data.describe()

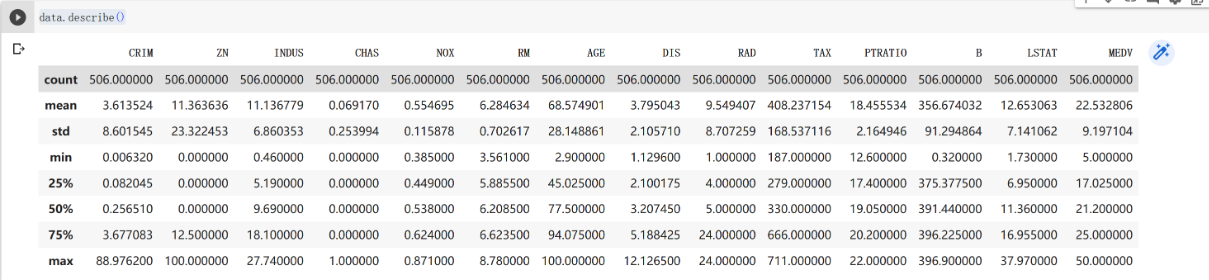
可以看出每一行的值都是正常的，没有异常值.
最后看一下有没有重复项。

1
data.duplicated() #检查每一行是否重复性，没有返回false，有返回true

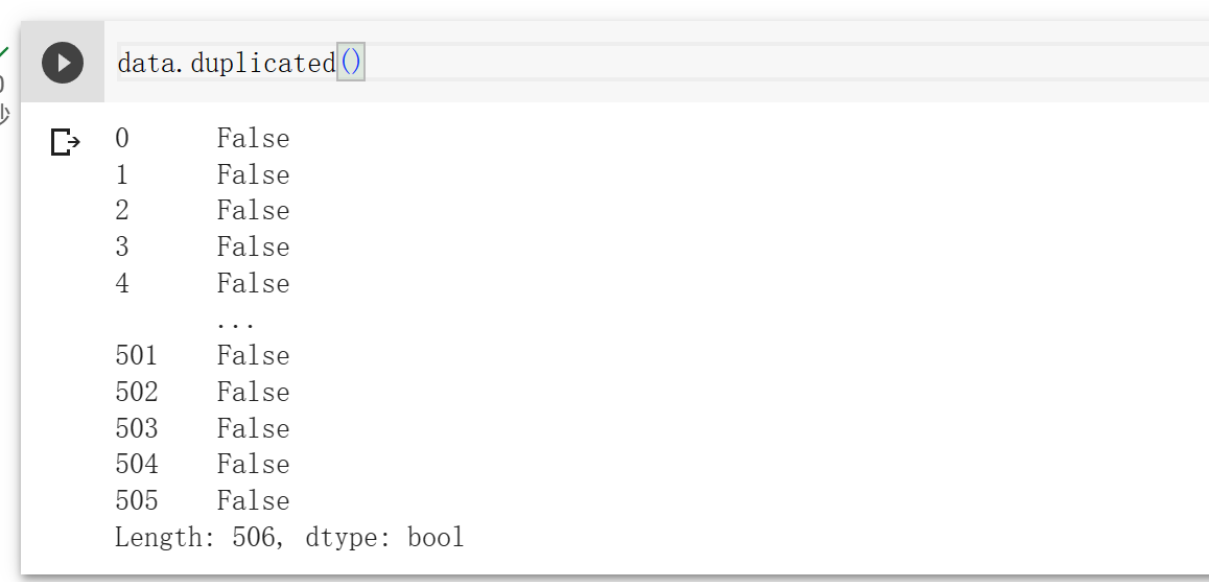
特征选择

由于参数太多，可能会影响后面模型的准确性，所以选择把不相关的特征删除。
就是删除相关系数小于0.5的特征，只保留大于等于0.5的特征。
首先计算每一个特征与标签的相关系数。

1
2
3
4
5
6
correlation_matrix = data.corr()  # 计算相关系数矩阵
correlation_with_label = correlation_matrix['MEDV']  # 提取目标变量(MEDV)与其他特征之间的相关系数

sorted_correlation = correlation_with_label.abs().sort_values(ascending=False)  # 按相关系数绝对值降序排列

print(sorted_correlation)

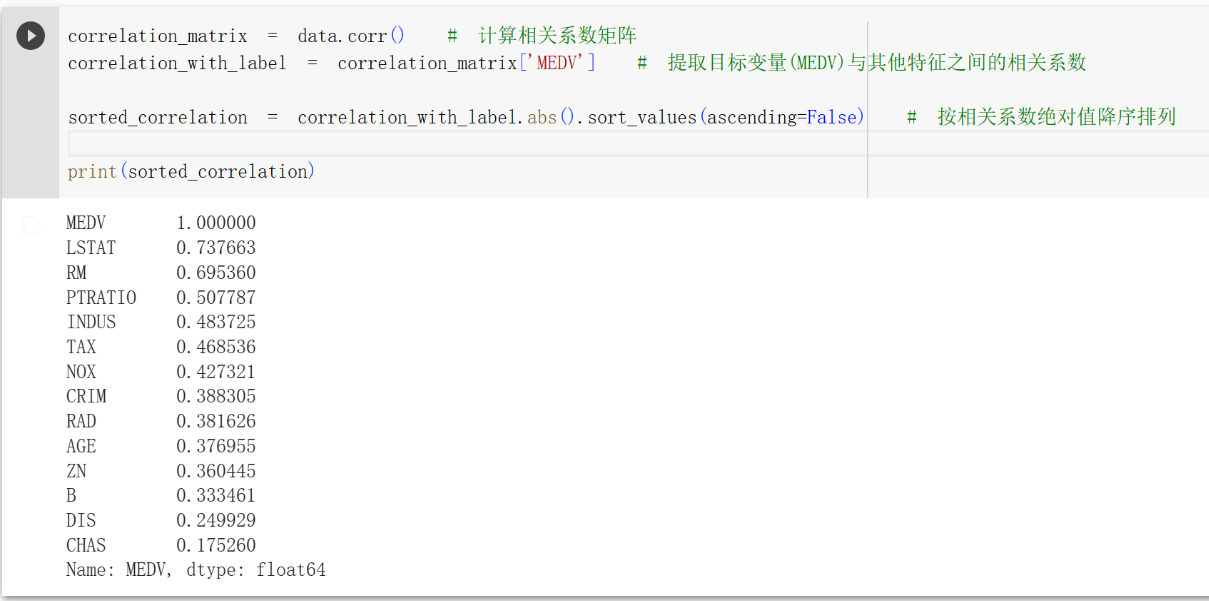
MEDV是本身，所以相关系数为1，我不知道怎么删除这个。除此之外，可以发现LSTAT、RM、PTRATIO 相关系数大于等于0.5了。
接下来画出这三个与标签的散点图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import matplotlib.pyplot as plt

plt.figure(figsize=(10, 6))

# 绘制'LSTAT'与'MEDV'的散点图
plt.scatter(data['LSTAT'], data['MEDV'])
plt.xlabel('LSTST')
plt.ylabel('MEDV')
plt.title('Scatter plot: LSTST vs MEDV')
plt.show()

plt.figure(figsize=(10, 6))

# 绘制'RM'与'MEDV'的散点图
plt.scatter(data['RM'], data['MEDV'])
plt.xlabel('RM')
plt.ylabel('MEDV')
plt.title('Scatter plot: RM vs MEDV')
plt.show()

plt.figure(figsize=(10, 6))

# 绘制'PTRATIO'与'MEDV'的散点图
plt.scatter(data['PTRATIO'], data['MEDV'])
plt.xlabel('PTRATIO')
plt.ylabel('MEDV')
plt.title('Scatter plot: PTRATIO vs MEDV')
plt.show()

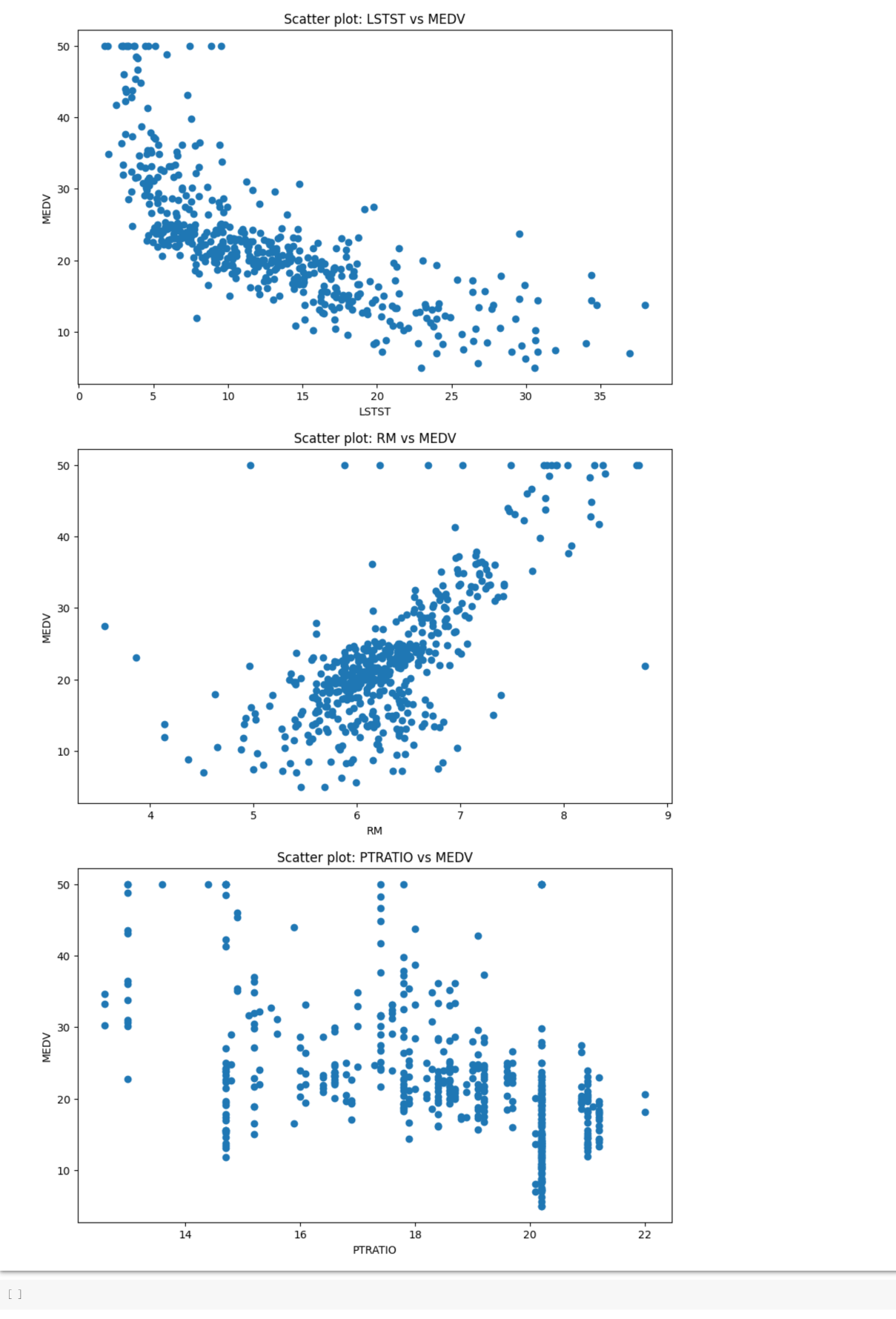
此时的 data 是一个Pandas 数据帧（DataFrame）对象，可以使用type()函数看一下
此时由于里面有的是字符串型，这里就需要用到咱们之前讲过的数据预处理里面的 处理缺失值。让字符串那一列变成一个特征，这样就变成了0、1.
接下来把data切片转化为 features（矩阵）、lables（向量）

1
2
3
4
5
6
7
8
import torch

data_features = data.iloc[:, [12, 5, 10]].values
data_labels = data.iloc[:, 13].values
features = torch.tensor(data_features, dtype=torch.float32)
labels = torch.tensor(data_labels, dtype=torch.float32)

features.shape, features, labels.shape, labels

特征放缩

特征放缩是什么？为什么要进行特征放缩呢？先来看一张图

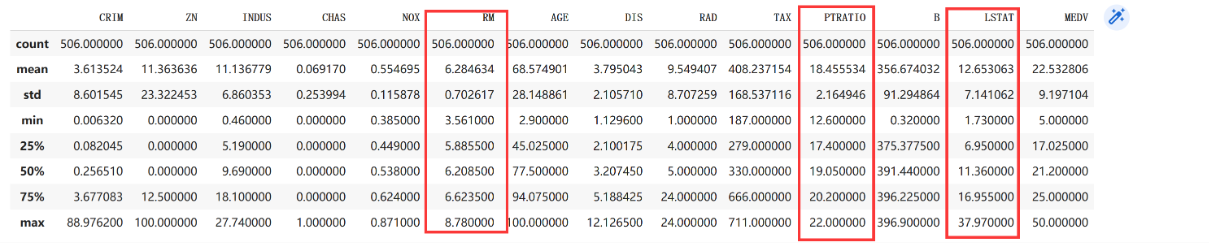
这三个是咱们的保留下来的特征，从图中咱们可以发现，这三个特征的平均值、最小值、最大值差的有点多。这样的差异会导致某些特征在模型训练中的权重更新过程中起主导作用，使得模型过于关注数值较大的特征，而忽略了其他特征的贡献。
通过特征放缩，可以将所有特征的数值调整到相似的尺度，减少数值差异对模型训练的影响，使得模型更加平衡地考虑不同特征的重要性。
而特征放缩有常用的有三个，标准化、Min-Max归一化方法、Min-Max归一化方法.
数据的特征放缩
这里采用的是Min-Max归一化方法。
将原始值减去最小值，并将差值除以最大值与最小值之间的差，从而获得新的归一化值。

1
2
3
4
5
6
from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler()
features = torch.tensor(scaler.fit_transform(features),dtype=torch.float32)
labels = torch.tensor(scaler.fit_transform(labels.reshape(-1, 1)),dtype=torch.float32)
features,labels

可以发现、特征、标签都被归一化0~1之间了。

读取数据集

原理：创建下标索引数组，然后原地打乱。最后通过 for循环来选择 batch_size个下标（不一定，有可能 i + batch_size越界，然后取num_example ），最后通过这些下标来返回batch_size 个特征、标签

1
2
3
4
5
6
7
8
9
def data_iter(batch_size,features,labels):
  num_example = len(features) #特征数量
  indices = list(range(num_example)) #生成一个list，存储下标
  random.shuffle(indices) #把下标打乱

  #开始批量返回batch_size个样本
  for i in range(0,num_example,batch_size):
    batch_indices = torch.tensor(indices[i:min(i + batch_size,num_example)]) #选择样本下标
    yield features[batch_indices],labels[batch_indices]
可以测试一下
1
2
3
4
5
batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

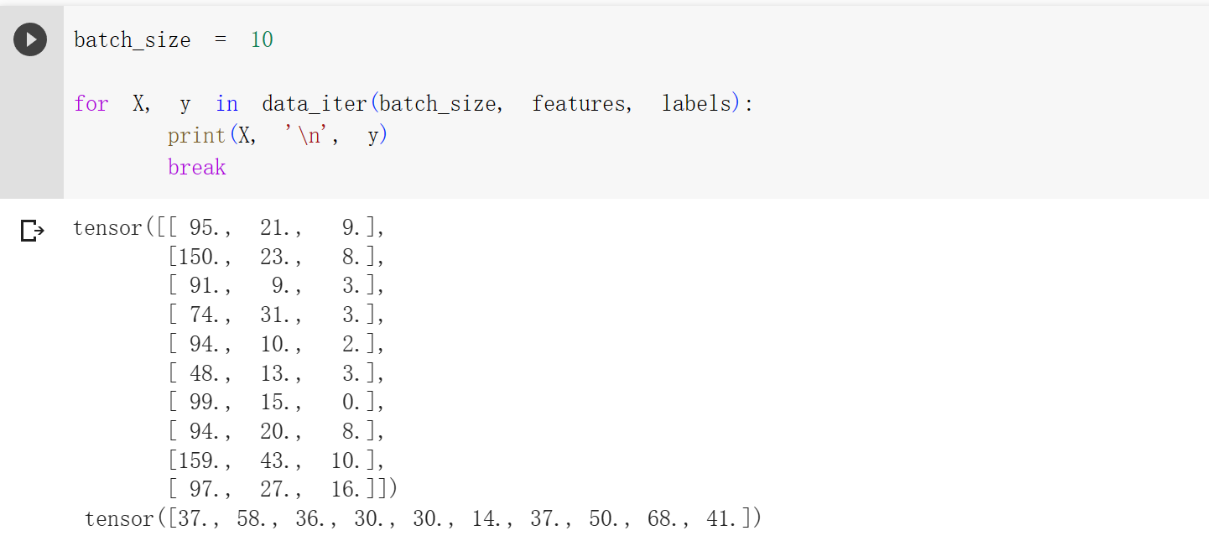
初始化模型参数

还是w随机，b设置为0

1
2
w = torch.normal(0, 0.01, size=(3,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

定义模型

由于这个是简单的线性回归, ，所以和之前推导的公式一样，直接写即可。

1
2
def linreg(X, w, b): 
    return torch.matmul(X, w) + b

定义损失函数

还是均分损失函数

1
2
def squared_loss(y_hat, y):  
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2 #没有除以均值，在计算梯度的时候再除
# 定义优化算法
1
2
3
4
5
def sgd(params, lr, batch_size):  #params是所有参数w、b的列表；lr为学习率、baatch_size为样本数量
    with torch.no_grad(): #上下文，关闭梯度计算，确保在更新参数时不会计算梯度。
        for param in params:
            param -= lr * param.grad / batch_size #更新
            param.grad.zero_() #清空梯度，因为梯度默认累积
# 训练 最后就是训练了，和之前一样
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
lr = 0.03 # 学习率
num_epochs = 3 #迭代周期

net = linreg 
loss = squared_loss

for epoch in range(num_epochs): #遍历迭代周期
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y) 
        l.sum().backward()
        sgd([w, b], lr, batch_size) 
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        score = mse_score(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}, score {float(score):f}')

1
2
def mse_score(y_hat, y):
    return ((y_hat - y) ** 2).mean().sqrt()

写在最后

其实这个和前面李沐老师讲的差不多，只不过多了一些数据处理操作。由于没有学过pandas，所以其中数据操作比较粗糙，敬请谅解！！！

  • Title: Linear Regression Experiment
  • Author: StarHui
  • Created at : 2023-06-21 21:01:17
  • Updated at : 2023-11-06 20:05:37
  • Link: https://renyuhui0415.github.io/post/Linear_Regression_Experiment.html
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
Linear Regression Experiment
  1. 前言
  2. 上传数据
  3. 数据预处理
    1. 数据清洗
    2. 特征选择
    3. 特征放缩
  4. 读取数据集
  5. 初始化模型参数
  6. 定义模型
  7. 定义损失函数
  8. 写在最后